7-贪心、回溯、动态规划

动态规划

淘宝的“双十一”购物节有各种促销活动，比如“满 200 元减 50 元”。假设你女朋友的购物车中有 n 个（n>100）想买的商品，她希望从里面选几个，在凑够满减条件的前提下，让选出来的商品价格总和最大程度地接近满减条件（200 元），这样就可以极大限度地“薅羊毛”。作为程序员的你，能不能编个代码来帮她搞定呢？

动态规划比较适合用来求解最优问题，比如求最大值、最小值等等。
最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，那我们也可以理解为，后面阶段的状态可以通过前面阶段的状态推导出来。
有重复子问题

javascript - 动态规划入门（以爬楼梯为例） - 个人文章 - SegmentFault 思否

方法二：备忘录算法

const map = new Map();
function getWays(n) {

if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;

if (map.has(n)) {
    return map.get(n);
}
const value = getWays(n-1) + getWays(n-2);
map.set(n, value);
return value; 

}

因为map里最终会存放n-2个键值对，所以空间复杂度为O(n),时间复杂度也为O(n)

继续想一想这就是最优的解决方案了吗？

我们回到一开始的思路，我们是假定前面的楼梯已经走完，只考虑最后一步，所以才得出来f(n) = f(n-1) + f(n-2)的递归式，这是一个置顶向下求解的式子
一般来说，按照正常的思路应该是一步一步往上走，应该是自底向上去求解才比较符合正常人的思维，我们来看看行不行的通

这是一开始走的一个和两个楼梯的走法数,即之前说的初始状态

这是进行了一次迭代得出了3个楼梯的走法，f(3)只依赖于f(1) 和 f(2)

继续看下一步

这里又进行了一次迭代得出了4个楼梯的走法，f(4)只依赖于f(2) 和 f(3)

我们发现每次迭代只需要前两次迭代的数据，不用像备忘录一样去保存所有子状态的数据

方法三：动态规划求解

function getWays(n) {

if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;

// a保存倒数第二个子状态数据，b保存倒数第一个子状态数据， temp 保存当前状态的数据
let a = 1, b = 2;
let temp = a + b;
for (let i = 3; i <= n; i++) {
    temp = a + b;
    a = b;
    b = temp; 
}
return temp; 

}

这是我们可以再看看当前的时间复杂度和空间复杂度
当前时间复杂度仍为O(n)，但空间复杂度降为O(1)
这就是理想的结果

0-1 背包

对于一组不同重量、不可分割的物品，我们需要选择一些装入背包，在满足背包最大重量限制的前提下，背包中物品总重量的最大值是多少呢？

规律是不是不好找？那我们就举个例子、画个图看看。我们假设背包的最大承载重量是 9。我们有 5 个不同的物品，每个物品的重量分别是 2，2，4，6，3。如果我们把这个例子的回溯求解过程，用递归树画出来，就是下面这个样子：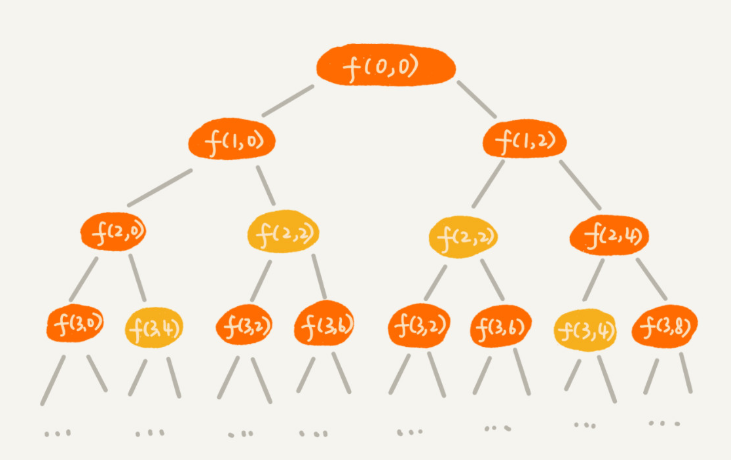

递归树中的每个节点表示一种状态，我们用（i, cw）来表示。其中，i 表示将要决策第几个物品是否装入背包，cw 表示当前背包中物品的总重量。比如，（2，2）表示我们将要决策第 2 个物品是否装入背包，在决策前，背包中物品的总重量是 2。
第 0 个（下标从 0 开始编号）物品的重量是 2，要么装入背包，要么不装入背包
从递归树中，你应该能会发现，有些子问题的求解是重复的，比如图中 f(2, 2) 和 f(3,4) 都被重复计算了两次。

private int maxW = Integer.MIN_VALUE; // 结果放到maxW中
private int[] weight = {2，2，4，6，3};  // 物品重量
private int n = 5; // 物品个数
private int w = 9; // 背包承受的最大重量
private boolean[][] mem = new boolean[5][10]; // 备忘录，默认值false
public void f(int i, int cw) { // 调用f(0, 0)
  if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了
    if (cw > maxW) maxW = cw;
    return;
  }
  if (mem[i][cw]) return; // 重复状态
  mem[i][cw] = true; // 记录(i, cw)这个状态
  f(i+1, cw); // 选择不装第i个物品
  if (cw + weight[i] <= w) {
    f(i+1,cw + weight[i]); // 选择装第i个物品
  }
}

总结

贪心、分治、回溯和动态规划
如果我们将这四种算法思想分一下类，那贪心、回溯、动态规划可以归为一类，而分治单独可以作为一类，因为它跟其他三个都不大一样。为什么这么说呢？前三个算法解决问题的模型，都可以抽象成我们今天讲的那个多阶段决策最优解模型，而分治算法解决的问题尽管大部分也是最优解问题，但是，大部分都不能抽象成多阶段决策模型。

回溯算法是个“万金油”。基本上能用的动态规划、贪心解决的问题，我们都可以用回溯算法解决。回溯算法相当于穷举搜索。穷举所有的情况，然后对比得到最优解。不过，回溯算法的时间复杂度非常高，是指数级别的，只能用来解决小规模数据的问题。对于大规模数据的问题，用回溯算法解决的执行效率就很低了。

尽管动态规划比回溯算法高效，但是，并不是所有问题，都可以用动态规划来解决。能用动态规划解决的问题，需要满足三个特征，最优子结构、无后效性和重复子问题。在重复子问题这一点上，动态规划和分治算法的区分非常明显。分治算法要求分割成的子问题，不能有重复子问题，而动态规划正好相反，动态规划之所以高效，就是因为回溯算法实现中存在大量的重复子问题。

然后，我讲了两种动态规划的解题思路。它们分别是状态转移表法和状态转移方程法。其中，状态转移表法解题思路大致可以概括为，回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 - 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码。状态转移方程法的大致思路可以概括为，找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码。

---

贪心算法

贪心算法有很多经典的应用，比如霍夫曼编码（Huffman Coding）、Prim 和 Kruskal 最小生成树算法、还有 Dijkstra 单源最短路径算法。最小生成树算法和最短路径算法我们后面会讲到，所以我们今天讲下霍夫曼编码，看看它是如何利用贪心算法来实现对数据压缩编码，有效节省数据存储空间的。

假设我们有一个可以容纳 100kg 物品的背包，可以装各种物品。我们有以下 5 种豆子，每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大，我们如何选择在背包中装哪些豆子？每种豆子又该装多少呢？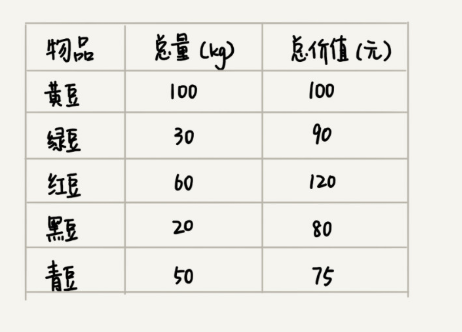

实际上，这个问题很简单，我估计你一下子就能想出来，没错，我们只要先算一算每个物品的单价，按照单价由高到低依次来装就好了。单价从高到低排列，依次是：黑豆、绿豆、红豆、青豆、黄豆，所以，我们可以往背包里装 20kg 黑豆、30kg 绿豆、50kg 红豆。

第一步，当我们看到这类问题的时候，首先要联想到贪心算法：针对一组数据，我们定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大。

类比到刚刚的例子，限制值就是重量不能超过 100kg，期望值就是物品的总价值。这组数据就是 5 种豆子。我们从中选出一部分，满足重量不超过 100kg，并且总价值最大。

回溯算法

回溯算法的核心就是试了再比，不行回退的思路。
回溯相当于穷举，使用合理的剪枝技巧减少穷举的数量

八皇后

我们有一个 8x8 的棋盘，希望往里放 8 个棋子（皇后），每个棋子所在的行、列、对角线都不能有另一个棋子。你可以看我画的图，第一幅图是满足条件的一种方法，第二幅图是不满足条件的。八皇后问题就是期望找到所有满足这种要求的放棋子方式。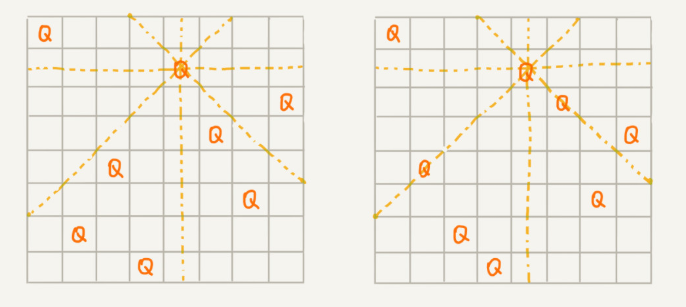

我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中，我们不停地检查当前的方法，是否满足要求。如果满足，则跳到下一行继续放置棋子；如果不满足，那就再换一种方法，继续尝试。

  int[] result = new int[8];//全局或成员变量,下标表示行,值表示queen存储在哪一列

    public void cal8queens(int row) { // 调用方式：cal8queens(0);
        if (row == 8) { // 8个棋子都放置好了，打印结果
            printQueens(result);
            return; // 8行棋子都放好了，已经没法再往下递归了，所以就return
        }
        for (int column = 0; column < 8; ++column) { // 每一行都有8中放法
            if (isOk(row, column)) { // 有些放法不满足要求
                result[row] = column; // 第row行的棋子放到了column列
                cal8queens(row + 1); // 考察下一行
            }
        }
    }

    private boolean isOk(int row, int column) {//判断row行column列放置是否合适
        int leftup = column - 1, rightup = column + 1;
        for (int i = row - 1; i >= 0; --i) { // 逐行往上考察每一行
            if (result[i] == column) return false; // 第i行的column列有棋子吗？
            if (leftup >= 0) { // 考察左上对角线：第i行leftup列有棋子吗？
                if (result[i] == leftup) return false;
            }
            if (rightup < 8) { // 考察右上对角线：第i行rightup列有棋子吗？
                if (result[i] == rightup) return false;
            }
            --leftup;
            ++rightup;
        }
        return true;
    }

    private void printQueens(int[] result) { // 打印出一个二维矩阵
        for (int row = 0; row < 8; ++row) {
            for (int column = 0; column < 8; ++column) {
                if (result[row] == column) System.out.print("Q ");
                else System.out.print("* ");
            }
            System.out.println();
        }
        System.out.println();
    }

穷举法

1. 穷举法的基本思想是根据题目的部分条件确定答案的大致范围，并在此范围内对所有可能的情况逐一验证，直到全部情况验证完毕。若某个情况验证符合题目的全部条件，则为本问题的一个解；若全部情况验证后都不符合题目的全部条件，则本题无解。穷举法也称为枚举法。

• 穷举法是一种针对于密码的破译方法。这种方法很像数学上的“完全归纳法”并在密码破译方面得到了广泛的应用。简单来说就是将密码进行逐个推算直到找出真正的密码为止。比如一个四位并且全部由数字组成其密码共有10000种组合，也就是说最多我们会尝试9999次才能找到真正的密码。利用这种方法我们可以运用计算机来进行逐个推算，也就是说用我们破解任何一个密码也都只是一个时间问题。

0-1 背包

链接
我们有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。我们现在期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量最大？
我们可以把物品依次排列，整个问题就分解为了 n 个阶段，每个阶段对应一个物品怎么选择。先对第一个物品进行处理，选择装进去或者不装进去，然后再递归地处理剩下的物品。

这里还稍微用到了一点搜索剪枝的技巧，就是当发现已经选择的物品的重量超过 Wkg 之后，我们就停止继续探测剩下的物品。你可以看我写的具体的代码。

   public int maxW = Integer.MIN_VALUE; //存储背包中物品总重量的最大值

    // cw表示当前已经装进去的物品的重量和；i表示考察到哪个物品了；
// w背包重量；items表示每个物品的重量；n表示物品个数
// 假设背包可承受重量100，物品个数10，物品重量存储在数组a中，那可以这样调用函数：
// f(0, 0, a, 10, 100)
    public void f(int i, int cw, int[] items, int n, int w) {
        if (cw == w || i == n) { // cw==w表示装满了;i==n表示已经考察完所有的物品
            if (cw > maxW) maxW = cw;
            return;
        }
        f(i + 1, cw, items, n, w);//当前物品不装进背包，第 11 行的递归调用表示不选择当前物品，直接考虑下一个（第 i+1 个），故 cw 不更新
        if (cw + items[i] <= w) {// 已经超过可以背包承受的重量的时候，就不要再装了
            f(i + 1, cw + items[i], items, n, w);//当前物品装进背包
        }
    }

0-1背包问题理解：假设三个物品，每个物品在考虑时有两种选择，1-放进包，0-不放。11行代码表示不放进包里。13行代码表示放进包里。三个物品遍历过程如下：
0 0 0 update maxW
0 0 1 update maxW
0 1 0 update maxW
0 1 1 update maxW
1 0 0 update maxW
1 0 1 update maxW
1 1 0 update maxW
1 1 1 update maxW

看看下面的图
算法复杂度2^n

回溯算法本质上就是枚举，优点在于其类似于摸着石头过河的查找策略，且可以通过剪枝少走冤枉路。它可能适合应用于缺乏规律，或我们还不了解其规律的搜索场景中。