2-递归、排序

如何在海量数据中快速查找某个数据？
建立索引，空间换时间，例如数据库，存储在硬盘
先思考后写；不要惧怕修改

递归

先写一个的解决方法，不想多层，写完再想如何多个

周末你带着女朋友去电影院看电影，女朋友问你，咱们现在坐在第几排啊？电影院里面太黑了，看不清，没法数，现在你怎么办？别忘了你是程序员，这个可难不倒你，递归就开始排上用场了。
于是你就问前面一排的人他是第几排，你想只要在他的数字上加一，就知道自己在哪一排了。但是，前面的人也看不清啊，所以他也问他前面的人。就这样一排一排往前问，直到问到第一排的人，说我在第一排，然后再这样一排一排再把数字传回来。直到你前面的人告诉你他在哪一排，于是你就知道答案了。
我们用递推公式将它表示出来就是这样的：

f(n)=f(n-1)+1 其中，f(1)=1

f(n) 表示你想知道自己在哪一排，f(n-1) 表示前面一排所在的排数，f(1)=1 表示第一排的人知道自己在第一排。有了这个递推公式，我们就可以很轻松地将它改为递归代码，如下：

int f(int n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

递归需要满足的三个条件

1. 一个问题的解可以分解为几个子问题的解
2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
3. 存在递归终止条件
   第一排的人不需要再继续询问任何人，就知道自己在哪一排，也就是 f(1)=1，这就是递归的终止条件。

调试递归

我们平时调试代码喜欢使用 IDE 的单步跟踪功能，像规模比较大、递归层次很深的递归代码，几乎无法使用这种调试方式。
调试递归:

1. 打印日志发现，递归值。
2. 结合条件断点进行调试。

   public class Recursion {
   	/**
   	 * 求和
   	 */
   	public static int summation(int num) {
   		if (num == 1) {
   			return 1;
   		}
   		return num + summation(num - 1);
   }  
   /**
    * 求二进制
    */
   public static int binary(int num) {
   	StringBuilder sb = new StringBuilder();
   	if (num > 0) {
   		summation(num / 2);
   		int i = num % 2;
   		sb.append(i);
   	}
   	System.out.println(sb.toString());
   	return -1;
   }
   
   /**
    * 求n的阶乘
    */
   public int f(int n) {
   	if (n == 1) {
   		return n;
   	} else {
   		return n * f(n - 1);
   	}
   }
   ```    
   
   ### 如何编写递归代码？
   
   写递归代码最关键的是写出递推公式，找到终止条件
   爬楼梯
   ```java
   int f(int n) {
     if (n == 1) return 1;
     if (n == 2) return 2;
     return f(n-1) + f(n-2);
   }

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

人脑几乎没办法把整个“递”和“归”的过程一步一步都想清楚。计算机擅长做重复的事情，所以递归正和它的胃口。
对于递归代码，这种试图想清楚整个递和归过程的做法，实际上是进入了一个思维误区。很多时候，我们理解起来比较吃力，主要原因就是自己给自己制造了这种理解障碍。那正确的思维方式应该是怎样的呢？

如果一个问题 A 可以分解为若干子问题 B、C、D，你可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A。而且，你只需要思考问题 A 与子问题 B、C、D 两层之间的关系即可，不需要一层一层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。屏蔽掉递归细节，这样子理解起来就简单多了。

因此，编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。
不要陷入思维误区。

递归代码要警惕堆栈溢出

函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

那么，如何避免出现堆栈溢出呢？

// 全局变量，表示递归的深度。
int depth = 0;
int f(int n) {
  ++depth；
  if (depth > 1000) throw exception;
  if (n == 1) return 1;
  return f(n-1) + 1;
}

但这种做法并不能完全解决问题，因为最大允许的递归深度跟当前线程剩余的栈空间大小有关，事先无法计算。如果实时计算，代码过于复杂，就会影响代码的可读性。所以，如果最大深度比较小，比如 10、50，就可以用这种方法，否则这种方法并不是很实用。

递归代码要警惕重复计算

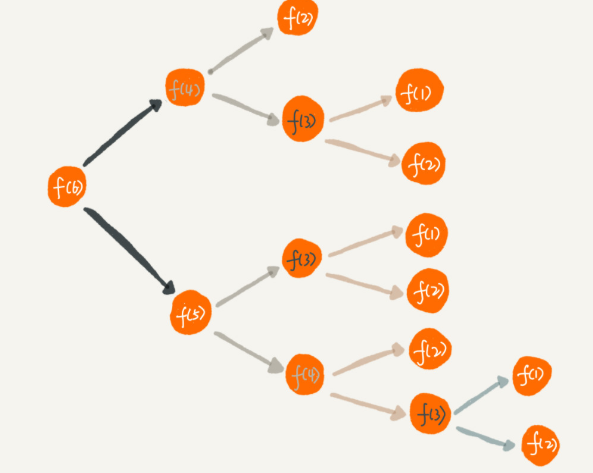
为了避免重复计算，我们可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)。当递归调用到 f(k) 时，先看下是否已经求解过了。如果是，则直接从散列表中取值返回，不需要重复计算，这样就能避免刚讲的问题了。

HashMap hasSolvedList = new HashMap();

public int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  
  // hasSolvedList可以理解成一个Map，key是n，value是f(n)
  if (hasSolvedList.containsKey(n)) {
	return hasSolvedList.get(n);
  }
  
  int ret = f(n-1) + f(n-2);
  hasSolvedList.put(n, ret);
  return ret;
}

电影院递归代码，空间复杂度并不是 O(1)，而是 O(n)。

怎么将递归代码改写为非递归代码？

递归有利有弊，利是递归代码的表达力很强，写起来非常简洁；而弊就是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题

电影院修改

int f(int n) {
  int ret = 1;
  for (int i = 2; i <= n; ++i) {
	ret = ret + 1;
  }
  return ret;
}

爬楼梯修改

但是这种思路实际上是将递归改为了“手动”递归，本质并没有变，而且也并没有解决前面讲到的某些问题，徒增了实现的复杂度。

如何找到“最终推荐人”？

推荐注册返佣金的这个功能我想你应该不陌生吧？现在很多 App 都有这个功能。这个功能中，用户 A 推荐用户 B 来注册，用户 B 又推荐了用户 C 来注册。我们可以说，用户 C 的“最终推荐人”为用户 A，用户 B 的“最终推荐人”也为用户 A，而用户 A 没有“最终推荐人”。

long findRootReferrerId(long actorId) {
  Long referrerId = select referrer_id from [table] where actor_id = actorId;
  if (referrerId == null) return actorId;
  return findRootReferrerId(referrerId);
}

不过在实际项目中，上面的代码并不能工作，为什么呢？这里面有两个问题。
第一，如果递归很深，可能会有堆栈溢出的问题。
第二，如果数据库里存在脏数据，我们还需要处理由此产生的无限递归问题。比如 demo 环境下数据库中，测试工程师为了方便测试，会人为地插入一些数据，就会出现脏数据。如果 A 的推荐人是 B，B 的推荐人是 C，C 的推荐人是 A，这样就会发生死循环。

第一个问题，我前面已经解答过了，可以用限制递归深度来解决。第二个问题，也可以用限制递归深度来解决。不过，还有一个更高级的处理方法，就是自动检测 A-B-C-A 这种“环”的存在。如何来检测环的存在呢？

排序

基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，如果我们在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

概念

原地

排序算法的内存消耗

算法的内存消耗可以通过空间复杂度来衡量，排序算法也不例外。不过，针对排序算法的空间复杂度，我们还引入了一个新的概念，原地排序（Sorted in place）。原地排序算法，就是特指空间复杂度是 O(1) 的排序算法。冒泡、插入、选择，都是原地排序算法。
==借助额外的存储空间==

稳定性

排序算法的稳定性

针对排序算法，我们还有一个重要的度量指标，稳定性。这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，==相等元素之间原有的先后顺序不变==。
我通过一个例子来解释一下。比如我们有一组数据 2，9，3，4，8，3，按照大小排序之后就是 2，3，3，4，8，9。这组数据里有两个 3。
经过某种排序算法排序之后，如果两个 3 的前后顺序没有改变，那我们就把这种排序算法叫作稳定的排序算法；如果前后顺序发生变化，那对应的排序算法就叫作不稳定的排序算法。

稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变

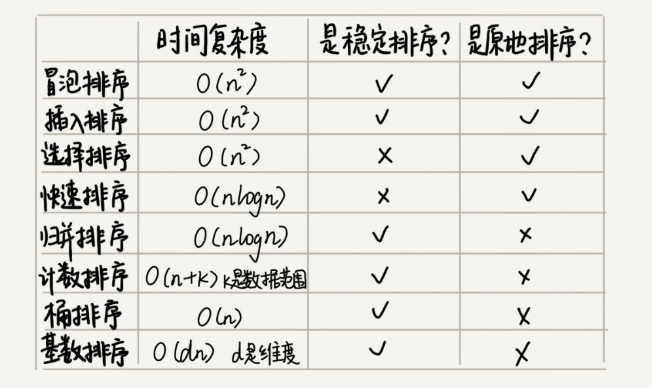
• 稳定排序有：插入排序，基数排序，归并排序 ，冒泡排序 ，基数排序。
• 不稳定的排序算法有：快速排序，希尔排序，简单选择排序，堆排序。

冒泡排序（Bubble Sort）

稳定、原地排序

我们要对一组数据 4，5，6，3，2，1，从小到大进行排序。经过一次冒泡操作之后，6 这个元素已经存储在正确的位置上。要想完成所有数据的排序，我们只要进行 6 次这样的冒泡操作就行了。

实际上，刚讲的冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。我这里还有另外一个例子，这里面给 6 个元素排序，只需要 4 次冒泡操作就可以了。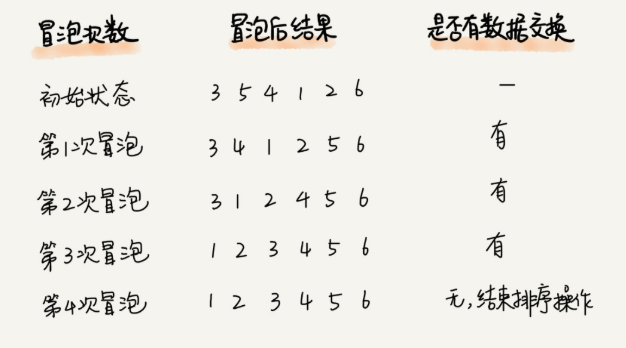

// 冒泡排序，a表示数组，n表示数组大小
public void bubbleSort(int[] a, int n) {
  if (n <= 1) return;
 
 for (int i = 0; i < n; ++i) {
	// 提前退出冒泡循环的标志位
	boolean flag = false;
	for (int j = 0; j < n - i - 1; ++j) { //-x：比较元素减少，-1：避免角标越界  
	  if (a[j] > a[j+1]) { // 交换
		int tmp = a[j];
		a[j] = a[j+1];
		a[j+1] = tmp;
		flag = true;  // 表示有数据交换      
	  }
	}
	if (!flag) break;  // 没有数据交换，提前退出
  }
}

插入排序（Insertion Sort）

稳定、原地排序

基本思想是每一步将一个待排序的记录，插入到前面已经排好序的有序序列中去，直到插完所有元素为止。

一个有序的数组，我们往里面添加一个新的数据后，如何继续保持数据有序呢？很简单，我们只要遍历数组，找到数据应该插入的位置将其插入即可。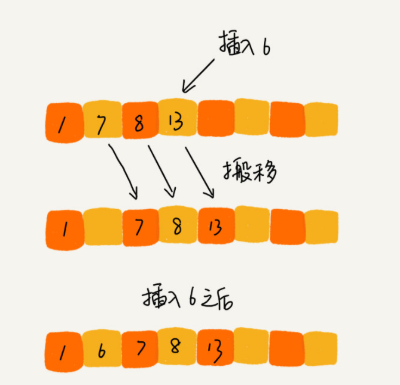

这是一个动态排序的过程，即动态地往有序集合中添加数据，我们可以通过这种方法保持集合中的数据一直有序。而对于一组静态数据，我们也可以借鉴上面讲的插入方法，来进行排序，于是就有了插入排序算法。

插入排序也包含两种操作，一种是元素的比较，一种是元素的移动。

当我们需要将一个数据 a 插入到已排序区间时，需要拿 a 与已排序区间的元素依次比较大小，找到合适的插入位置。找到插入点之后，我们还需要将插入点之后的元素顺序往后移动一位，这样才能腾出位置给元素 a 插入。

// 插入排序，a表示数组，n表示数组大小
public void insertionSort(int[] a, int n) {
  if (n <= 1) return;

  for (int i = 1; i < n; ++i) {
	  //待插入元素
	int value = a[i];
	int j = i - 1;
	// 查找插入的位置
	for (; j >= 0; --j) {
	  if (a[j] > value) {
		a[j+1] = a[j];  // 数据移动，将大于temp的往后移动一位
	  } else {
		break;
	  }
	}
	a[j+1] = value; // 插入数据
  }
}

插入排序和冒泡排序的时间复杂度相同，都是 O(n2)，在实际的软件开发里，为什么我们更倾向于使用插入排序算法而不是冒泡算法呢？

冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个。我们来看这段操作：冒泡排序中数据的交换操作：

冒泡排序中数据的交换操作：
if (a[j] > a[j+1]) { // 交换
   int tmp = a[j];
   a[j] = a[j+1];
   a[j+1] = tmp;
   flag = true;
}

插入排序中数据的移动操作：
if (a[j] > value) {
  a[j+1] = a[j];  // 数据移动
} else {
  break;
}

我们把执行一个赋值语句的时间粗略地计为单位时间（unit_time），然后分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序，需要 K 次交换操作，每次需要 3 个赋值语句，所以交换操作总耗时就是 3* K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。

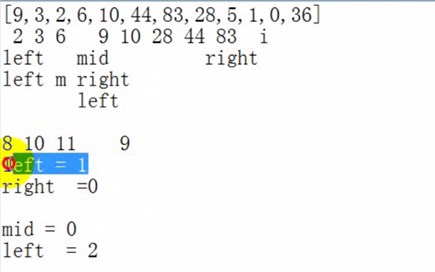
二分法插入排序

二分法插入排序是在插入第i个元素时，对前面的0～i-1元素进行折半，先跟他们中间的那个元素比，如果小，则对前半再进行折半，否则对后半进行折半，直到left>right，然后以左下标为标准，左及左后边全部后移，然后左位置前插入该数据。

二分法没有排序，只有查找。所以当找到要插入的位置时。移动必须从最后一个记录开始，向后移动一位，再移动倒数第2位，直到要插入的位置的记录移后一位。

private static void sort(int[] a) {
	// {4, 6, 8, 7, 3, 5, 9, 1}
	// {4, 6, 7, 8, 3, 5, 9, 1}
	for (int i = 1; i < a.length; i++) {
		int temp = a[i];//7
		int left = 0;
		int right = i - 1;//2
		int mid = 0;
		//确定(找到)要插入的位置
		while (left <= right) {
			//先获取中间位置
			mid = (left + right) / 2;
			if (temp < a[mid]) {
				//如果值比中间值小，让right左移到中间下标-1，舍弃右边
				right = mid - 1;
			} else {//7  6
				//如果值比中间值大,让left右移到中间下标+1，舍弃左边
				left = mid + 1;//2
			}
		}
		for (int j = i - 1; j >= left; j--) {
			//以左下标为标准，左及左后边全部后移，然后左位置前插入该数据。
			a[j + 1] = a[j];
		}
		if (left != i) {//如果相等，不需要移动
			//左位置插入该数据
			a[left] = temp;
		}
	}
}

希尔排序（O(n^1.3)）

• 希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。
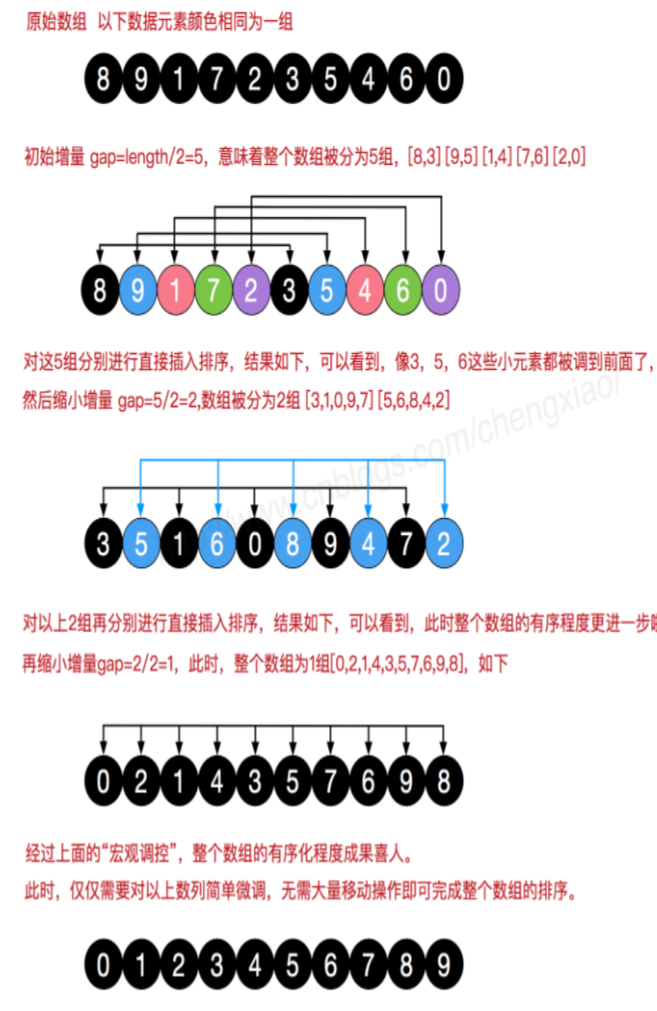
• 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
• 先取一个小于 n 的整数 d1作为第一个增量，把数组的全部记录分组。所有距离为 d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量 d2<d1重复上述的分组和排序，直至所取的增量 =1 ( < …<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

public void heer(int[] a) {
	int d = a.length / 2;//默认增量
	while (true) {
		for (int i = 0; i < d; i++) {
			for (int j = i; j + d < a.length; j += d) {
				//i=0  j=0,4
				//i=1  j=1,5
				int temp;
				if (a[j] > a[j + d]) {
					temp = a[j];
					a[j] = a[j + d];
					a[j + d] = temp;
				}
			}
		}
		if (d == 1) {
			break;
		}
		d--;
	}
}

选择排序（Selection Sort）

基本思想为每一趟从待排序的数据元素中选择最小（或最大）的一个元素作为首元素，直到所有元素排完为止
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

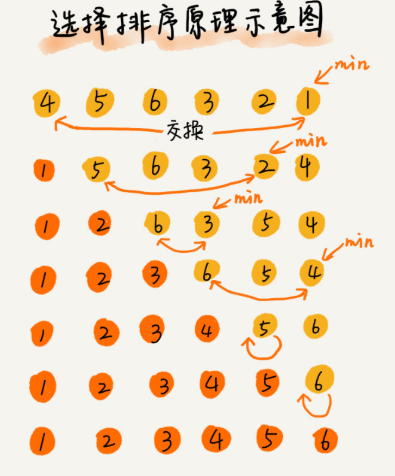
那选择排序是稳定的排序算法吗？
比如 5，8，5，2，9 这样一组数据，使用选择排序算法来排序的话，第一次找到最小元素 2，与第一个 5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。正是因此，相对于冒泡排序和插入排序，选择排序就稍微逊色了。

public void selectSort(int[] array) {
	int min;
	int tmp;
	for (int i = 0; i < array.length; i++) {
		min = array[i];
		//里面for第一次出来0，并且排在最前面，然后从i=1开始遍历
		for (int j = i; j < array.length; j++) {
			if (array[j] < min) {
				min = array[j];//记录最小值  3
				tmp = array[i];//9
				array[i] = min;//3
				array[j] = tmp;//9
			}
		}
	}
	for (int num : array) {
		System.out.println(num);
	}
}

归并排序（Merge Sort）

冒泡排序、插入排序、选择排序这三种排序算法，它们的时间复杂度都是 O(n2)，比较高，适合小规模数据的排序。今天，我讲两种时间复杂度为 O(nlogn) 的排序算法，归并排序和快速排序。这两种排序算法适合大规模的数据排序

稳定，但是，归并排序并没有像快排那样，应用广泛，这是为什么呢？因为它有一个致命的“弱点”，那就是归并排序不是原地排序算法。
这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。

归并排序的原理：分治法

归并排序和快速排序都用到了分治思想，非常巧妙。
如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。
分治法的基本思想是：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题的解组合为原问题的解。

分治思想跟我们前面讲的递归思想很像。是的，分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧，这两者并不冲突。

如何用递归代码来实现归并排序

写递归代码的技巧就是，分析得出递推公式，然后找到终止条件，最后将递推公式翻译成递归代码。所以，要想写出归并排序的代码，我们先写出归并排序的递推公式。

递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))

终止条件：
p >= r 不用再继续分解

代码

public class MergeSort {
	public void mergeSort(int[] a, int left, int right) {
		if (left < right) {
			int middle = (left + right) / 2;
			mergeSort(a, left, middle);//左边归并排序，使得左子序列有序
			mergeSort(a, middle + 1, right);//右边归并排序，使得右子序列有序
			merge(a, left, middle, right);//将两个有序子数组合并操作
		}
	}

	private void merge(int[] a, int left, int middle, int right) {//left0,mid0,right1
		//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
		int[] tmpArray = new int[a.length];
		int rightStart = middle + 1;//右序列指针
		int leftStart = left;//左序列指针，用来拷贝到原数组中
		int temp = left;//临时数组指针
		//比较两个小数组相应下标位置的数组大小，小的先放进新数组
		while (left <= middle && rightStart <= right) {
			if (a[left] <= a[rightStart]) {
				//相当于tmpArray[third]=a[left];third++;left++三步合一步
				tmpArray[temp++] = a[left++];
			} else {
				tmpArray[temp++] = a[rightStart++];
			}
		}
		//如果左边还有数据需要拷贝，把左边数组剩下的拷贝到新数组
		while (left <= middle) {
			tmpArray[temp++] = a[left++];
		}
		//如果右边还有数据......
		while (rightStart <= right) {
			tmpArray[temp++] = a[rightStart++];
		}
		//将temp中的元素全部拷贝到原数组中
		while (leftStart <= right) {
			a[leftStart] = tmpArray[leftStart++];
		}
	}

	public static void main(String[] args) {
		MergeSort mergeSort = new MergeSort();
		int[] a = new int[]{9, 7, 6, 5, 4, 3, 2, 1};
		mergeSort.mergeSort(a, 0, a.length - 1);
		for (int n : a) {
			System.out.print(" " + n);
		}
	}
}

快速排序（Quicksort）

快排是一种原地、不稳定的排序算法。

快排利用的也是分治思想。乍看起来，它有点像归并排序，但是思路其实完全不一样。我们待会会讲两者的区别。现在，我们先来看下快排的核心思想。

基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。利用分治法可将快速排序的分为三步：

1. 在数据集之中，选择一个元素作为”基准”（pivot）。
2. 所有小于”基准”的元素，都移到”基准”的左边；所有大于”基准”的元素，都移到”基准”的右边。这个操作称为分区 (partition) 操作，分区操作结束后，基准元素所处的位置就是最终排序后它的位置。
3. 对”基准”左边和右边的两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

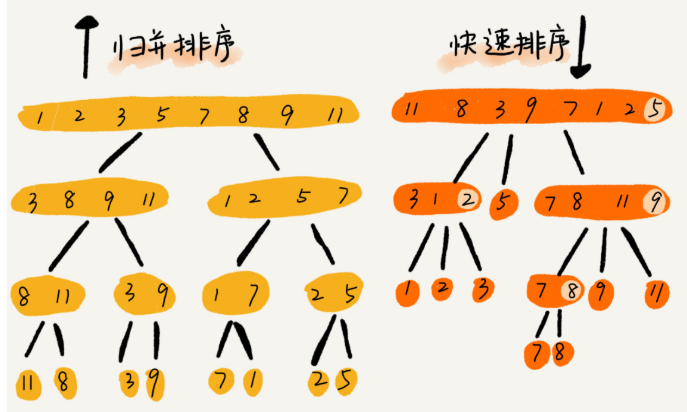
快速排序和归并排序对比

归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

public class QuickSort {

	public void quick(int[] a) {
		if (a.length > 0) {
			quickSort(a, 0, a.length - 1);
		}
	}

	/**
	 * 快速排序
	 * @param a
	 * @param low  低位
	 * @param high 高位
	 */
	private void quickSort(int[] a, int low, int high) {
		if (low < high) {
			int middle = getMiddle(a, low, high);
			//递归排比第一个基数小的数和大的数
			quickSort(a, 0, middle - 1);
			quickSort(a, middle + 1, high);
		}
	}

	/**
	 * 获取中间下标
	 *
	 * @param a
	 * @param low
	 * @param high
	 * @return
	 */
	private int getMiddle(int[] a, int low, int high) {
		int temp = a[low];//基准元素
		while (low < high) {//第二次3，9
			while (low < high && a[high] >= temp) {
				high--;
			}
			a[low] = a[high];//将比基数小的数放到基数前面///用个数字想一下就明白了
			while (low < high && a[low] <= temp) {
				low++;
			}
			a[high] = a[low];//将比基数大的数放到基数后面
		}
		a[low] = temp;//插入到排序后正确的位置，low就是基数应该在的位置
		return low;
	}
}

无序数组中的第 K 大元素

O (n) 时间复杂度

快排核心思想就是分治和分区，我们可以利用分区的思想，来解答开篇的问题：O(n) 时间复杂度内求无序数组中的第 K 大元素。比如，4， 2， 5， 12， 3 这样一组数据，第 3 大元素就是 4。
我们选择数组区间 A[0…n-1] 的最后一个元素 A[n-1] 作为 pivot，对数组 A[0…n-1] 原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。

如果 p+1=K，那 A[p] 就是要求解的元素；如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1] 区间，我们再按照上面的思路递归地在 A[p+1…n-1] 这个区间内查找。同理，如果 K<p+1，那我们就在 A[0…p-1] 区间查找。

理解分治，小问题

int kthLargest = leetCode.findKthLargest(new int[]{4, 2, 5, 12, 3}, 3);
//倒数
class Solution {
    public int findKthLargest(int[] nums, int k) {
        int len = nums.length;
        int left = 0, right = len - 1;
        int pivot = 0;
        while (len - k != (pivot = partition(nums, left, right))) {
        //4所在的问题就是2，那就找到了
        //第k大应该在第K位，找每个数字应该在的位置，正好第0个4就是第K位，就找到了
            if (pivot < len - k) {//在后面
                left = pivot + 1;
                right = len - 1;
            } else {
                left = 0;
                right = pivot - 1;
            }
        }
        return nums[pivot];
    }
    private int partition(int[] nums, int left, int right) {
        int pivot = nums[left];
        while (left < right) {
            while (left < right && nums[right] >= pivot)
                right--;
            nums[left] = nums[right];
            while (left < right && nums[left] <= pivot)
                left++;
            nums[right] = nums[left];
        }
        nums[left] = pivot;
        return left;
    }
}

为什么上述解决思路的时间复杂度是 O(n)？
第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。依次类推，分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。
如果我们把每次分区遍历的元素个数加起来，就是：n+n/2+n/4+n/8+…+1。这是一个等比数列求和，最后的和等于 2n-1。所以，上述解决思路的时间复杂度就为 O(n)。

桶排序（Bucket sort）

时间复杂度是 O(n) 的排序算法：桶排序、计数排序、基数排序。因为这些排序算法的时间复杂度是线性的，所以我们把这类排序算法叫作线性排序（Linear sort）。之所以能做到线性的时间复杂度，主要原因是，这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。

按照惯例，我先给你出一道思考题：如何根据年龄给 100 万用户排序？ 你可能会说，我用上一节课讲的归并、快排就可以搞定啊！是的，它们也可以完成功能，但是时间复杂度最低也是 O(nlogn)。有没有更快的排序方法呢？让我们一起进入今天的内容！

桶排序，顾名思义，会用到“桶”，核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

桶排序的时间复杂度为什么是 O(n) 呢
如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n* log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

桶排序看起来很优秀，那它是不是可以替代我们之前讲的排序算法呢？
要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。

桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。

比如说我们有 10GB 的订单数据，我们希望按订单金额（假设金额都是正整数）进行排序，但是我们的内存有限，只有几百 MB，没办法一次性把 10GB 的数据都加载到内存中。这个时候该怎么办呢？

计数排序（Counting sort）

我个人觉得，计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

我们都经历过高考，高考查分数系统你还记得吗？我们查分数的时候，系统会显示我们的成绩以及所在省的排名。如果你所在的省有 50 万考生，如何通过成绩快速排序得出名次呢？

考生的满分是 900 分，最小是 0 分，这个数据的范围很小，所以我们可以分成 901 个桶，对应分数从 0 分到 900 分。根据考生的成绩，我们将这 50 万考生划分到这 901 个桶里。桶内的数据都是分数相同的考生，所以并不需要再进行排序。我们只需要依次扫描每个桶，将桶内的考生依次输出到一个数组中，就实现了 50 万考生的排序。因为只涉及扫描遍历操作，所以时间复杂度是 O(n)。

计数排序的算法思想就是这么简单，跟桶排序非常类似，只是桶的大小粒度不一样

先行排序再看看

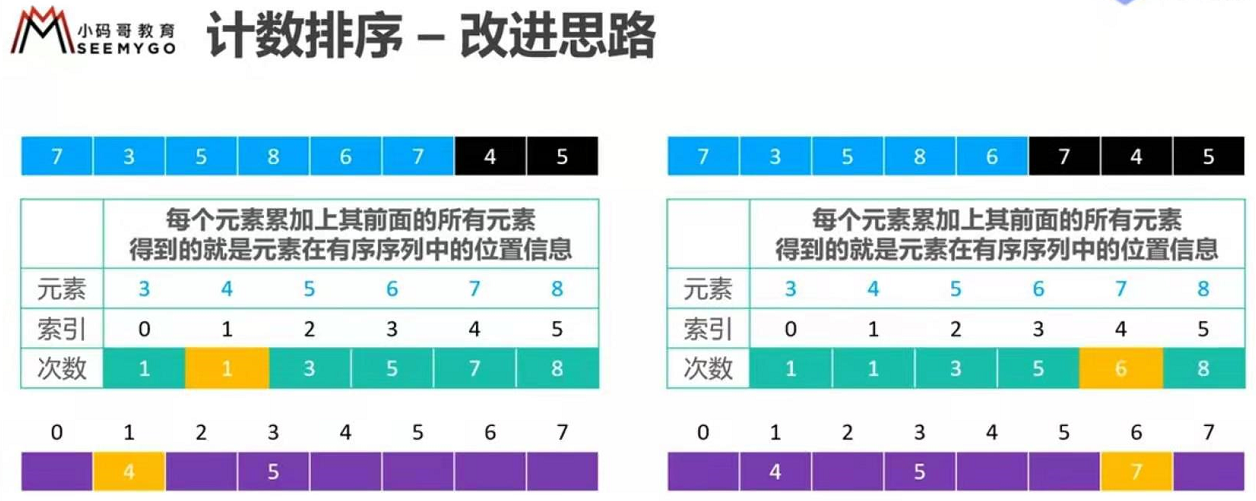
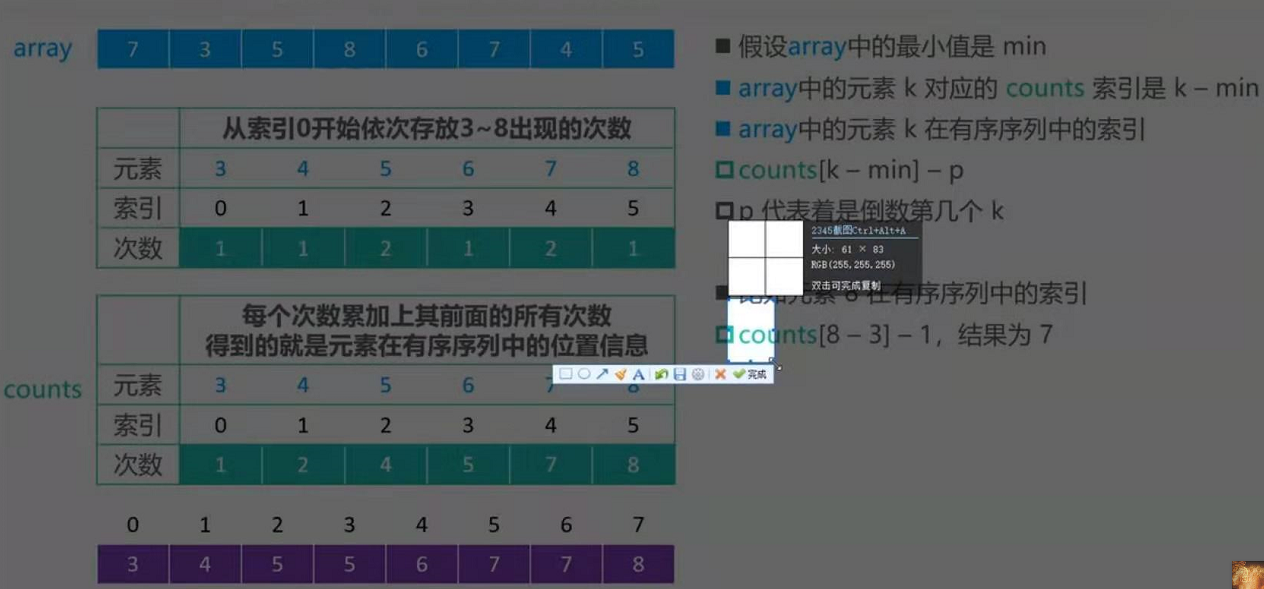
基数排序

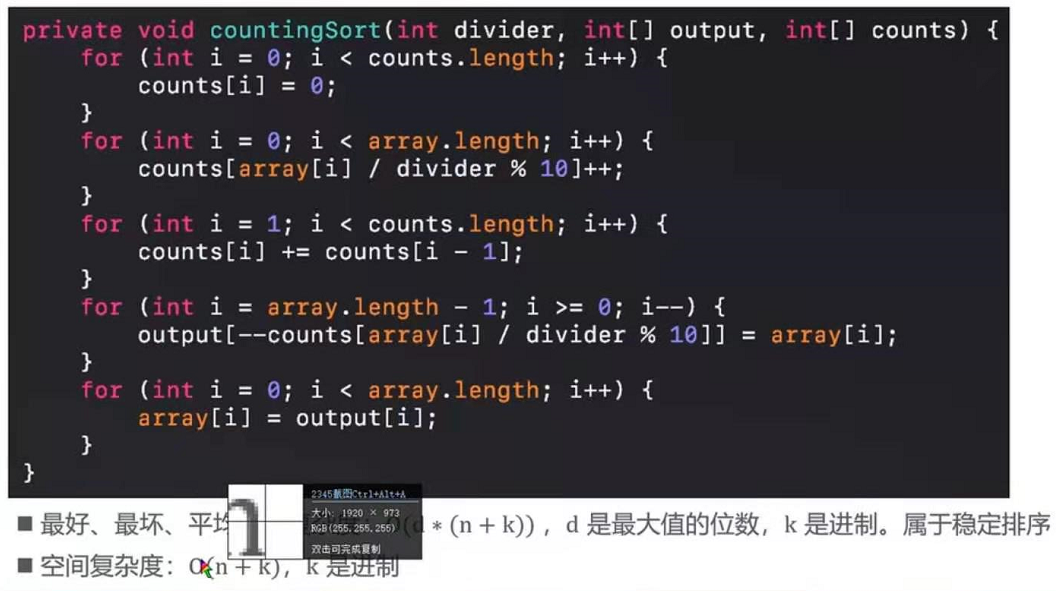
如何实现一个通用的、高性能的排序函数？

如果对小规模数据进行排序，可以选择时间复杂度是 O(n2) 的算法；如果对大规模数据进行排序，时间复杂度是 O(nlogn) 的算法更加高效。所以，为了兼顾任意规模数据的排序，一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。
Java 语言采用堆排序实现排序函数，C 语言使用快速排序实现排序函数。

我们知道，快排在最坏情况下的时间复杂度是 O(n2)，而归并排序可以做到平均情况、最坏情况下的时间复杂度都是 O(nlogn)，从这点上看起来很诱人，那为什么它还是没能得到“宠信”呢？

归并排序并不是原地排序算法，空间复杂度是 O(n)。所以，粗略点、夸张点讲，如果要排序 100MB 的数据，除了数据本身占用的内存之外，排序算法还要额外再占用 100MB 的内存空间，空间耗费就翻倍了。

如何优化快速排序？

为什么最坏情况下快速排序的时间复杂度是 O(n2) 呢？我们前面讲过，如果数据原来就是有序的或者接近有序的，每次分区点都选择最后一个数据，那快速排序算法就会变得非常糟糕，时间复杂度就会退化为 O(n2)。实际上，这种 O(n2) 时间复杂度出现的主要原因还是因为我们分区点选的不够合理。
最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。

1. 三数取中法
2. 随机法

在 qsort() 插入排序的算法实现中，也利用了这种编程技巧。虽然哨兵可能只是少做一次判断，但是毕竟排序函数是非常常用、非常基础的函数，性能的优化要做到极致。